Analoge Grundlagen - Teil 2: Delta-Sigma(ΔƩ)-ADCs und wie man ihre digitalen Fähigkeiten nutzt

Anmerkung der Redaktion: Analog/Digital-Wandler (ADCs) verbinden die analoge mit der digitalen Welt und sind somit eine grundlegende Komponente jedes elektronischen Systems, das eine Verbindung zur realen Welt herstellt. Sie sind auch ein entscheidender Bestimmungsfaktor für die Leistung eines Systems. In dieser Reihe werden die Grundlagen der ADCs, ihre verschiedenen Arten und ihre Anwendung untersucht. Teil 1 dieser Serie über analoge Grundlagen diskutierte SAR-ADCs. Hier werden in Teil 2 die Delta-Sigma(ΔƩ)-Wandler diskutiert. Teil 3 befasst sich mit den Pipeline-ADCs. Teil 4 zeigt, wie Delta-Sigma-ADCs extrem rauscharme Ergebnisse erzeugen können. Teil 5 befasst sich mit schwierigen Eingangs-Treiberfragen für SAR-ADCs.

Wie bei dem in Teil 1 besprochenen Analog/Digital-Wandler (ADC) mit sukzessivem Approximationsregister (SAR) zu sehen ist, kann die Herausforderung hoher Präzision einer analogen Sensorsignalkette - mit mehrfacher Verstärkung, Signalkonditionierung und komplexen analogen Filterstufen, die alle in einen SAR-ADC eingespeist werden - zu analogen Fehltritten führen. Entwickler können auch am Ende mit einer teuren, dicht bestückten Leiterplatte dastehen.

Zusätzlich, beginnend mit den ultra-niedrigen Sensorsignalen, bringt der Ausgang jeder analogen Stufe in der Signalkette Fehler ein, die sich am digitalen Ausgang des Wandlers als ein niedriges Signal-Rausch-Verhältnis (SNR) und hohe Verzerrungsfehler manifestieren. Die Entwickler solcher Systeme müssen einen Schritt zurücktreten und das Paradigma der hochpräzisen Sensor-ADCs neu überdenken.

Die Lösung der mit einem hochpräzisen Sensorsystem verbundenen Probleme besteht darin, eine ADC-Topologie zu wählen, die das kleine Sensorsignal schnell digitalisiert und die verrauschten analogen Funktionen von Verstärkung und Filterung digital implementiert. Dies ist die Rolle des Delta-Sigma(ΔƩ)-ADCs.

Dieser Artikel beschreibt kurz die grundlegende Funktion eines ΔƩ-ADCs und die interne Analog/Digital-Wandlungsmechanik am Beispiel eines Analog/Digital-Frontends AD4110-1 mit Universaleingang von Analog Devices. Von dort aus wird ein tieferer Blick auf die umgebende Signalkette geworfen und kritische Spezifikationen für ein geeignetes Datenerfassungssystem geliefert.

Die Struktur eines ΔƩ-ADC

Kurz vor der Jahrhundertwende stahl der ΔƩ-ADC das analoge Rampenlicht. Mit der weitverbreiteten Annahme der fortschrittlichen ΔƩ-Technologie begannen die primären analogen Signal- und Berechnungsprozesse in der digitalen Domäne zu liegen. Eine Untersuchung des integrierten Schaltkreises (IC) des ΔƩ-ADCs zeigt, dass über 80% der Komponenten des ICs digitale Funktionen ausführen. Das Nebenprodukt der überwiegend digitalen Schaltungen ist Robustheit und ein geringer Platzbedarf.

Wie war das möglich? Es beginnt mit der direkten Digitalisierung von analogen Niederspannungssignalen. Im digitalen Bereich können digitale Schaltungen die analoge Filterung fast vollständig ersetzen und gleichzeitig alle erforderlichen Verstärkungsfunktionen ausführen (Abbildung 1). Auch digitale Schaltungen schrumpfen mit jedem Halbleiterprozessknoten.

Abbildung 1: Ein ΔƩ enthält fast alle notwendigen Schaltungen zur Filterung und Verstärkung. In diesem Beispiel erfasst und digitalisiert ein ΔƩ-ADC die Spannung des Temperaturdetektors mit kleinem Widerstand (RTD). Anschließend verwendet er interne digitale Signalverstärkung und Filterung, um ein rauscharmes digitales 24-Bit-Ergebnis zu erzielen. (Bildquelle: A Baker's Dozen)

In Abbildung 1 besteht das 24-Bit-ΔƩ-ADC-System aus einem analogen Eingang, einer zentralen digitalen Engine und einem digitalen I/O-Terminal. Der Wandler erfasst das Niederspannungs-RTD-Signal und erzeugt durch digitale Filterung eine vollständige digitale 24-Bit-Darstellung des analogen Eingangs. Ein analoger Verstärkungsblock - normalerweise dominant in SAR-ADC-Schaltungen - existiert hier nicht, und das einzige analoge Filter ist die Kombination aus R₁ und C₁. Ja, dies ist ein einfacher, kostengünstiger Filter erster Ordnung!

Wie der ΔƩ-ADC arbeitet

Die Basistopologie eines ΔƩ-ADC besteht aus einem ΔƩ-Modulator in Serie mit einem digitalen Filter. Über diese Basistopologie hinaus weisen die meisten ΔƩ-ADCs eine Vielzahl weiterer Merkmale auf. Alle ΔƩ-Wandler verfügen jedoch über diesen wesentlichen Kern (Abbildung 2).

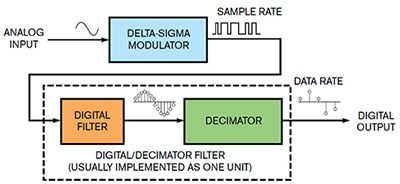Abbildung 2: Auf das Wesentliche reduziert, verfügt jeder ΔƩ-ADC über einen ΔƩ-Modulator, einen digitalen Filter und einen Dezimator. (Bildquelle: EDN)

In Abbildung 2 kann die Eingabe sinusförmig oder DC sein; diese Diskussion wird sich auf eine sinusförmige Eingabe konzentrieren. Der ΔƩ-Modulator digitalisiert eine Sinuswelle mit einem einzigen Zyklus zu einem 1-Bit-Stream. Die Ausgangsabtastfrequenz des ΔƩ-Modulators ist Fs. Obwohl die 1-Bit-Modulatorwandlung ein hohes Quantisierungsrauschen zu haben scheint, wird das Signalrauschen tatsächlich in die höheren Frequenzen „geformt“. Dies ebnet den Weg für eine rauscharme, hochauflösende Umwandlung am Ausgang des Digitalfilters.

Am Ausgang des Modulators akkumuliert der Digitalfilter die 1-Bit-Ergebnisse des ΔƩ-Modulators und führt Filterberechnungen durch. Das Ausgangssignal des Digitalfilters spiegelt das analoge Eingangssignal digital wider, während es mit einer Ausgangsfrequenz Fs weitergeführt wird. Das Signal befindet sich nun ausschließlich im digitalen Bereich. Ein digitaler Tiefpassfilter oder Dezimationsfilter dämpft höherfrequentes Rauschen und verlangsamt die Ausgangsdatenrate 1/Fd. Der Digital/Dezimator-Filter tastet und filtert den 1-Bit-Code-Stream des Modulators zu einem langsameren Multi-Bit-Code.

Während die meisten Konverter nur eine Abtastrate haben, hat der ΔƩ Konverter zwei: die Eingangsabtastfrequenz (Fs) und die Ausgangsdatenfrequenz (Fd). Das Verhältnis dieser beiden Frequenzvariablen definiert das Systemdezimationsverhältnis (DR) gemäß Gleichung 1:

 Gleichung 1

ΔƩ-Modulator

Der ΔƩ-Modulator führt die eigentliche Analog/Digital-Wandlung durch, indem er einen Strom von 1-Bit-Codes erzeugt. Dieser Prozess beginnt an einem Differenzverstärker (Abbildung 3).

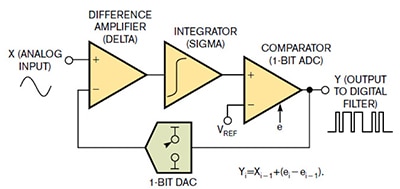Abbildung 3: Die ΔƩ-ADC-Modulator-Eingangsstufe erfasst das Delta zwischen dem analogen Eingang und dem Rückkopplungs-DAC. Die zweite Stufe implementiert eine Integratorfunktion oder Sigma auf dem Analogsignal. (Bildquelle: EDN)

In Abbildung 3 überträgt der Differenzverstärker (Delta) das Analogsignal an einen Integrator (Sigma). Am Ausgang des Integrators unterscheidet ein Komparator bei einer sehr hohen Abtastrate (1/Fs) zwischen dem Ausgang des Integrators und einer Spannungsreferenz (V_REF). Zusätzlich gibt der Komparator den 1-Bit-Strom an den 1-Bit-Digital/Analog-Wandler (DAC). Der Modulator misst dann die Differenz zwischen dem analogen Eingangssignal und dem analogen Ausgang des Rückkopplungs-DAC.

Der ΔƩ-Modulator formt das Rauschen durch die Wirkung des Integrators und der DAC-Rückkopplungsschleife zu höheren Frequenzen aus. Die Formel in Abbildung 3 (unten rechts) zeigt die Übertragungsgleichung als Y_i = X_i-1 + (e_i - e_i-1). Der Modulator digitalisiert das Eingangssignal (X_i) zu einem 1-Bit-Ausgangscode (Y_i) mit einem Quantisierungsrauschen (e_i). Konkret entspricht der Ausgang des Modulators (Y_i) dem Eingang (X_i-1) plus dem Quantisierungsrauschen (e_i - e_i-1). Die Formel zeigt das Quantisierungsrauschen als Differenz zwischen dem aktuellen Fehler (e_i) minus dem vorherigen Fehler des Modulators (e_i-1).

Digital- und Dezimationsfilter

Die Mittelwertbildung ist eine Form der digitalen Filterung, die in industriellen ΔƩ-ADCs mit niedriger Geschwindigkeit üblich ist. Fast alle industriellen ΔƩ-ADCs enthalten eine Klasse von Filtern zur Mittelwertbildung, die sinc-Filter genannt werden, und die ein linear-phasiges finites Impuls-Ansprechverhalten (FIR) verwenden, das ein digitaler Tiefpassfilter ist (Abbildung 4).

Abbildung 4: Die Koeffizienten (b_x) in diesem FIR-Digitalfilter zur Mittelwertbildung sind alle gleich eins. (Bildquelle: DigiKey)

In Abbildung 4 ist der Ausgangsbitstrom des Modulators der Eingang zu diesem digitalen Filter, und der Abtasttakt des Modulators bestimmt die Verzögerungszeit. Die Koeffizienten von Abbildung 4 (b_x) für FIR-Filter sind alle gleich eins. Mit diesem Mittelungsalgorithmus erzeugt der FIR-Digitalfilter eine rauscharme, digitale 24-Bit-Darstellung des analogen Eingangs in Abbildung 3, wobei die Abtastwerte mit der Abtastrate des Modulators (1/Fs) auftreten. Der Dezimationsfilter reduziert dann die Ausgabedatenrate unter Verwendung des DR.

In der Literatur bezieht sich der Begriff „Dezimierung“ auf den militärischen Akt der systematischen Entfernung unerwünschter Soldaten. Die Dezimierung in der digitalen Elektronik verwendet dasselbe Konzept, um die Ausgangsdatenrate (1/Fd) des digitalen Signals durch die DR zu reduzieren. Der schnelle und digitale Weg, dies zu erreichen, besteht darin, systematisch einige der Ausgabeproben des digitalen Filters zu verwerfen (Abbildung 5).

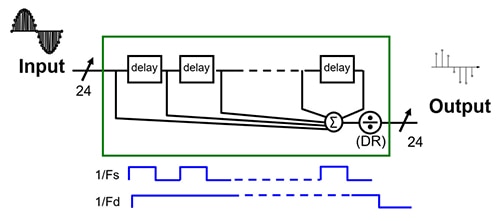Abbildung 5: Der Dezimierungsprozess reduziert systematisch die Anzahl der digitalen 24-Bit-Ausgänge um einen Faktor der Ausgangsdatenrate (1/Fd, am unteren Bildrand) geteilt durch die Abtastrate (1/Fs). (Bildquelle: DigiKey)

Der Dezimierungsprozess in Abbildung 5 dezimiert die Ausgangsdatenrate (1/Fd) durch die DR gemäß Gleichung 1.

Die Ereignisse durch den Digital- und Dezimationsfilter reduzieren effektiv das Rauschen des ΔƩ-ADCs (Abbildung 6).

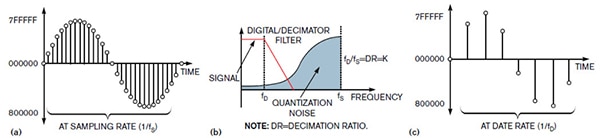Abbildung 6: Hier dargestellt, der digitale Filterausgang (a) im Zeitbereich; der rauschförmige Modulatorausgang, der der Tiefpaßfunktion des Dezimationsfilters überlagert ist (b); und das Ausgangssignal des Dezimators im Zeitbereich (c). (Bildquelle: EDN)

Abbildung 6 zeigt das digitale Signal, wie es den Digital-/Dezimationsfilter durchläuft. Der 24-Bit-Ausgang des Digitalfilters (Abbildung 6(a)) läuft mit der gleichen Rate wie die Abtastrate des Modulators (1/Fs). Der Modulator hat das Quantisierungsrauschen bereits in höhere Frequenzen geformt (Abbildung 6(b)), so dass der Digital/Dezimationsfilter den niederfrequenten Anteil des Ausgangssignals erfasst. Der Ausgang des Dezimationsfilters (Abbildung 6(c)) erzeugt eine niederfrequente digitale Darstellung des ursprünglichen Analogsignals.

Digitale Erweiterung

Der ΔƩ-ADC ist hauptsächlich im digitalen Bereich angesiedelt. Jetzt können digital programmierbare Verstärkungsstufen, Stromquellen, Kurzschluss- oder Leerlauf-Eingangssignalindikatoren und verschiedene serielle Ausgangsschnittstellen einfach hinzugefügt werden (Abbildung 7).

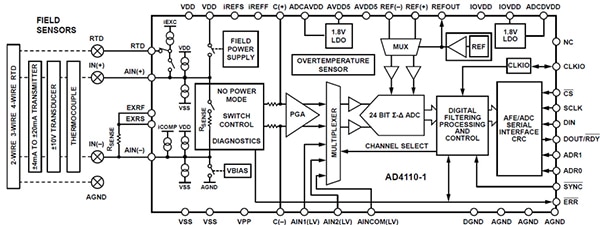Abbildung 7: Der AD4110-1 von Analog Devices bietet mehrere analoge Frontend-Funktionen für industrielle Prozesssteuerungssysteme. (Bildquelle: Analog Devices)

Abbildung 7 zeigt, dass der ΔƩ-ADC AD4110-1 von Analog Devices zahlreiche digitale Verbesserungen aufweist, darunter programmierbare Eingangsterminals, Diagnosefunktionen und flexible Datenraten. Die eingabebereiten Sensorschnittstellen umfassen RTD- und Thermoelement-Temperatursensoren.

Der AD4110-1 hat den grundlegenden Kern eines ΔƩ-ADCs, aber die digitale Betonung des Geräts ermöglicht eine Reihe von digitalen Funktionen, so dass der AD4110-1 jetzt ein universelles analoges Frontend (AFE) ist.

Wie bei einem üblichen ΔƩ-ADC ist der AD4110-1 in der Lage, extrem niedrige Spannungen von Thermoelementen, RTDs und Brücken zu digitalisieren. Während diese Funktionen oft zusätzliche Erregerschaltungen erfordern, sind sie beim AD4110-1 bereits an Bord integriert.

Zum Beispiel erfordert der RTD eine Präzisionsstromquelle, die ratiometrisch zur Spannungsreferenz des Wandlers ist (Abbildung 8).

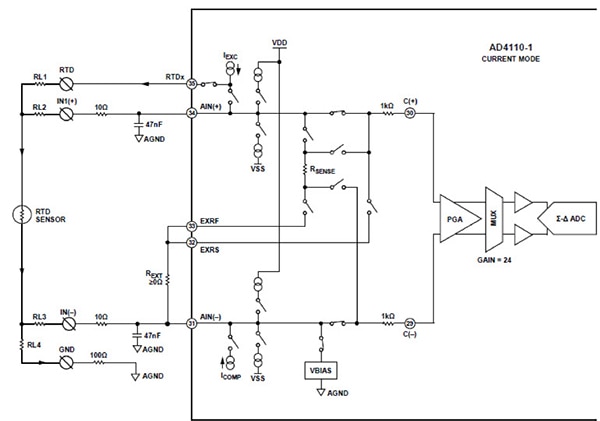Abbildung 8: Geeignete Drahtverbindungen für einen Vier-Draht-RTD und den AD4110-1 ΔƩ-ADC. Der RTD-Erregerstrom ist in sechs Stufen zwischen 0,1 Milliampere (mA) und 1 mA programmierbar. (Bildquelle: Analoge Geräte)

In Abbildung 8 enthält der AD4110-1 einen Erregerstrom, der mit Hilfe des PGA_RTD_CTRL-Registers des Wandlers auf sechs Stufen zwischen 0,1 mA und 1 mA programmiert werden kann. Der Erregerstrom für den RTD-Widerstand kommt von Pin 35. Der Wandler erfasst den Spannungsabfall über den RTD über die hochohmigen Eingänge der Pins 34 und 31. Der Verstärker mit programmierbarer Verstärkung (PGA) des AD4110-1 bietet 16 programmierbare Verstärkungen von 0,2 bis 24 Volt/Volt. Mit dieser Funktion ist der Entwickler in der Lage, den Eingangssensor auf den Eingangsbereich des AD4110-1 weiter zu ergänzen. Weitere Hilfsfunktionen sind Pull-up-/Pull-down-Ströme zur Erkennung eines offenen Drahtes (nützlich bei Thermoelementen), Verstärkungskalibrierung und Korrekturkoeffizienten.

Fazit

Der ΔƩ-ADC eliminiert komplexe analoge Frontend-Schaltungen und liefert ein hochauflösendes, digital gemitteltes, rauscharmes digitales Ausgangssignal unter Verwendung eines Frontend-Modulators, eines FIR-Digitalfilters und eines Dezimationsfilters. Da ein Großteil der Schaltungen in digitaler Form vorliegt, kann sie mit fortschrittlichen digitalen Prozessknoten leicht skaliert werden, und es können mehr Funktionen hinzugefügt werden, während gleichzeitig ein kleinerer Footprint und eine reduzierte Platinenkomplexität beibehalten werden.

Der ΔƩ-ADC AD4110-1 von Analog Devices macht sich die Eigenschaften dieser ADC-Architektur zunutze. Der AD4110-1 verfügt über den grundlegenden Kern eines ΔƩ-ADCs, aber die digitale Betonung des Geräts ermöglicht eine Reihe von digitalen Funktionen, so dass der AD4110-1 jetzt ein universelles AFE und wirklich RTD- und Thermoelement-tauglich ist.